こんにちは!ケンけんです。前回は、数字の最大最小を順序関係にまで一般化し、数では現れなかった極大・極小を扱いました。
今回は、半順序集合の上界・下界・それらの最小最小を扱います。
キーワード:上界下界・上限下限
導入
つまり、$x$の範囲が定まることで範囲外の数についての順序も定まっていると言えます。従って、$X=\{x \in \mathbb{R}|2\leq x \leq 4 \}$について次のことが言えます。
- $Y=\{y \in \mathbb{R}|y \leq 2\}$は任意の$x \in X$以下の数全体
- $Z=\{y \in \mathbb{R}|4 \leq y\}$は任意の$x \in X$以上の数全体
このような$Y$の元を「$X$の下界」、$Z$の元を「$X$の上界」と呼び微積分学で登場します。
そんでこれ、何に使うのと思うでしょう。なぜなら考えている数から外れた数のことなのであまり意味がないように思えます。しかしこの2つのはずれものは、非常に重要なものです。例えば次のような極限を考えましょう。
$\lim_{n \rightarrow \infty}\frac{1}{n}=0$
高校時代の数列の極限(数学Ⅲ)にて求めたことがあるでしょう。このとき、「限りなく近づく」などとごまかしながら話を進めたと思います。しかし数学は誰にも等しく納得できる・理解できるものでなければなりません。命題や集合を言語から記号化してきたようにここも記号化する必要があります。この近づくと言うことをどのようにして説明するのか。残念ながら集合の道具だけでは説明できず、長さのような構造(距離位相)を作る必要があります。
今回は位相空間論ではないので深入りはしませんが、例の数列についてイメージをしてみましょう。
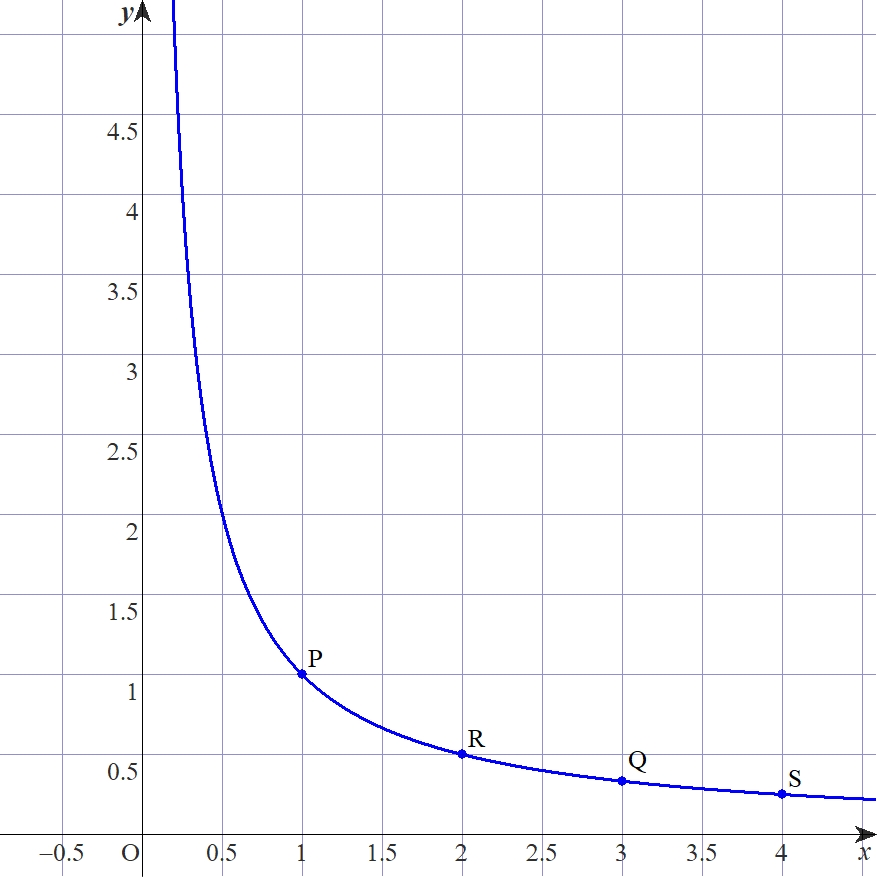
例:関数$\frac{1}{x}$のグラフ
上のグラフは分数関数$\frac{1}{x}$のものですだが、数列$\frac{1}{n}$はこのグラフの横軸が自然数の時の点に位置します。高校数学では、極限では$0$に近づいているから極限値も$0$としていました。でも考えてみてください。$\frac{1}{n}$は絶対に$0$になりません。つまり、数列の取り得る値の集合は$\{\frac{1}{n}|0 < \frac{1}{n}\}$だと言えます。この集合の下界は$0$以下の数すべてでありその全体は「$x \leq 0$」だと言えます。つまりこの数列の極限値だと思っていた値は下界の最大値です。
これはもちろん偶然ではありません。一般に$\frac{1}{n}$のような「下界を持つ単調減少する数列での極限値は、下界の最大値と一致する」定理が存在します。(有界単調列の収束性)「上界を持つ単調増加する数列の極限値」は、上界の最小値と一致します。これは上の定理と同じ主張です。これは、実数の連続性の同値条件の一つで極限を考えるときに登場します。
数列の極限を考えるときには、上界・下界の最小・最大が必要になるのはわかりました。しかし、集合に最大最小が必ずしも存在するとは限りませんでした。そのために極大・極小が表れたのですから。ですが、上界・下界を考えることでべき集合の部分集合の特徴を外部から見ることができます。
$X=\{1,2,3\}$のべき集合について部分集合として$Y=\{\emptyset , \{1\} , \{2\} , \{1,2\} , \{1,3\} , \{2,3\}\}$を考えます。
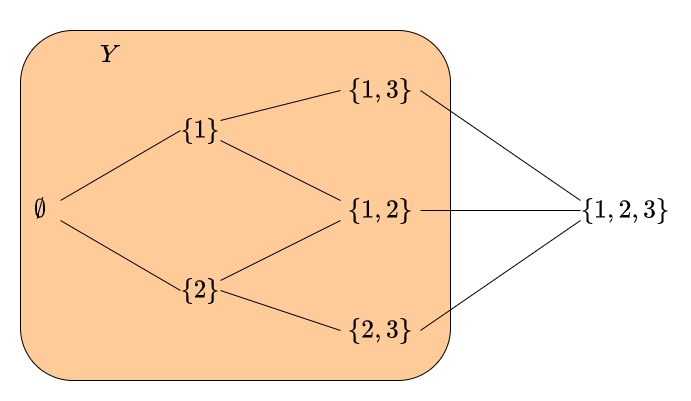
例:$X=\{1,2,3\}$について$Y=\{\emptyset , \{1\} , \{2\} , \{1,2\} , \{1,3\} , \{2,3\}\}$の包含関係の図
このとき、$X$がまさしく$Y$の上界です。これは、$X$が3つの元しか持っていないから簡単ですが、上の図だけでも上界の存在によってそれと包含関係を持つ元が少なくとも一つとれます。従って、枝分かれした半順序集合の中に極大元らしきものが取れることが図を書かなくても予想できそうです。この現象を全順序部分集合のみ考えることで、定理として証明可能です。それがツォルンの補題です。
$U$:普遍集合 $\emptyset \neq X \subset U$
$(X \leq)$:半順序集合
- 任意の全順序部分集合$S$は$X$の中で上界を持つ $\Rightarrow$ $(X \leq)$は極大元を持つ
この「上界を持つ半順序集合」は整列集合という名前がついています。
この補題はあの選択公理・整列可能性定理と同値な命題として有名です。
そのため証明には、この2つのいずれかの仮定が必要です。
ここから、上界は極大元の存在について影響があると言えるでしょう。考えたい集合を直接見ずに、それを順序関係で上から抑えることで調べることができるわけです。
上界下界
それでは定義します。と言っても名前を付けるだけですが。
$U$:普遍集合 $Y \subset X \subset U$ $x \in X$
$(X,\leq)$:半順序集合 $(Y,\leq)$:半順序集合
- $x$は$Y$の上界($upper bound$)$\overset{def}{\iff} \forall a \in Y(a \leq x)$
- $x$は$Y$の下界($lower bound$)$\overset{def}{\iff} \forall a \in Y(x \leq a)$
$U(Y)$:$Y$の上界全体の集合 $L(Y)$:$Y$の下界全体の集合
- $Y$は上に有界$\overset{def}{\iff} U(Y)\neq \emptyset$
- $Y$は下に有界$\overset{def}{\iff} L(Y)\neq \emptyset$
- $x$は$Y$の上限($supremum$)$\overset{def}{\iff} x$:$U(Y)$の最小元
- $x$は$Y$の下限($infimum$) $\overset{def}{\iff} x$:$L(Y)$の最大元
この上限下限は、最大元最小元なので存在しない場合もあります。しかし存在する場合は、数列の極限のように有用な道具になります。
「有界」というワードを聞くと、何かしらおおわれていると言ったことをイメージするといいです。
例えば、「$1<x$」の場合は$1$が下界(下限でもある)なので下に有界になります。上に有界な場合は「$x \leq 11$」などの場合は$11$が上界になるので上に有界です。従って、有界であるとは不等号で、考えている数$x$が挟まれているかです。
上(下)に有界という考えは、単調増加(単調減少)な数列・関数と相性が非常にいいです。先ほどの$\frac{1}{n}$の場合は下に有界な単調減少列でした。ここでは上に有界な単調増加列を考えます。
上界$a$が存在するする比較する数$x$に対して、常に「$x \leq a$」という関係が成り立っています。なので、単調増加の数列$a_{n} \in \{x \in \mathbb{R}|x \leq a\}$ の場合は$|a_{n}-a|$がどんどん小さくなっていきます。このとき極限を考えると、上限の$a$に近づいていると説明できそうですね。
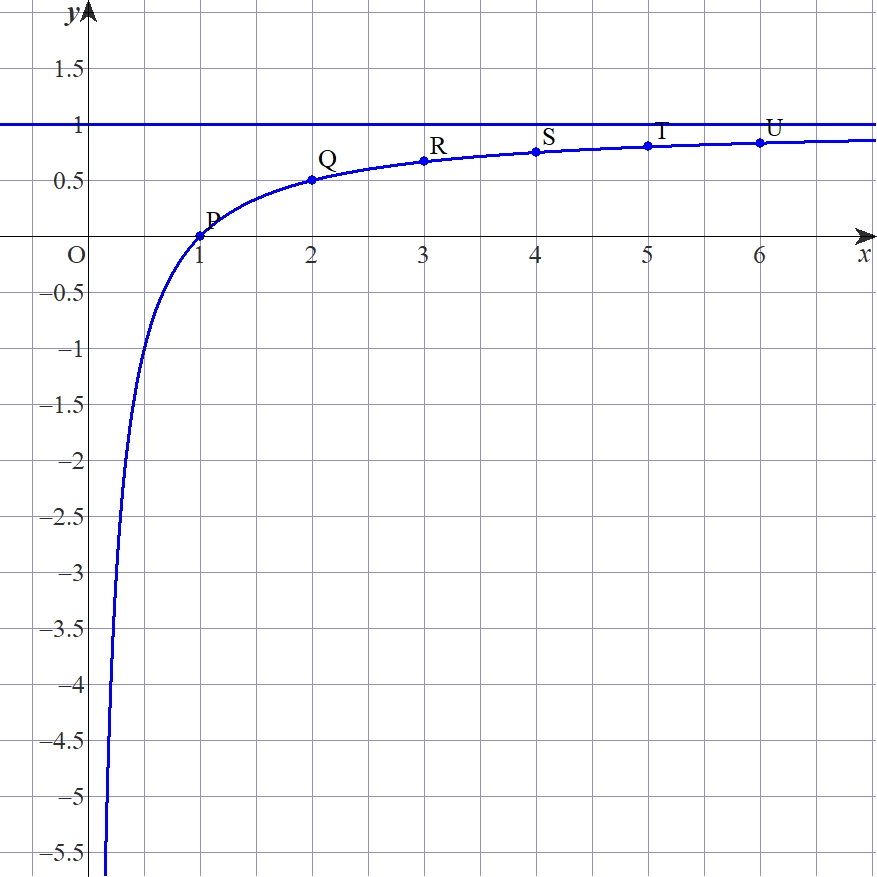
例:$y=1$と$y=1-\frac{1}{x}$のグラフ
上の図からわかるように、単調増加列$a_{n}=1-\frac{1}{n}$が上限の$1$に近づいていきます。この長さ$|a_{n}-1|$が、どんどん近づきほとんどぺしゃんこになる状況によって極限が定まります。有界である場合は天井(または床)にぶつからないすれすれで近づいているようなものです。有界性は、その中で動くもの(数列・関数)の動きを制限するものとして有用なのです。
「$0\leq x \leq 1$」は、上にも下にも有界なので単に「有界である」と呼びます。
上限と下限のイメージ
導入にて単調減少な数列の極限値が、下界の下限になることを確認しました。ここから、少し上限と下限について考えてみます。
数の範囲「$a<x<b$」の場合、上界と下界の範囲は「$b \leq x$」、「$x \leq a$」となります。
従って集合として$X=\{x \in \mathbb{R}|a<x<b\}$、$U(X)=\{x \in \mathbb{R}|b \leq x\}$、$L(X)=\{x \in \mathbb{R}|x \leq a\}$となります。よって、$X$の上限は$b$であり、$X$の下限は$a$となります。
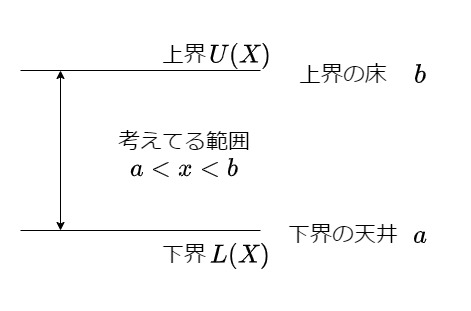
図:$a<x<b$と上限下限のイメージ
上の図では、両端$a,b$を含んでいませんが上限と下限がすぐにわかります。「$a\leq x \leq b$」の場合は、最大値$b$、最小値$a$を持ちこれらは上限下限と一致することが定義からわかります。なぜなら、$b,a$はそれぞれ$X$の上界下界であることは変わらず、それらの最小元最大元であることも変わらないからです。
また一般の場合では、上限と下限の存在も明らかではなく存在しない場合もあり得ます。ですが実数には次の連続性の公理から存在が保証されます。
$\mathbb{R}$:実数全体の集合 $\emptyset \neq X \subset \mathbb{R}$
$\mathbb{R}$は数の大小により全順序集合
- $X$は上に有界$\Rightarrow X$は上限を持つ
- $X$は下に有界$\Rightarrow X$は下限を持つ
従って次のことがわかります。
$\mathbb{R}$:実数全体の集合 $\emptyset \neq X \subset \mathbb{R}$
$\mathbb{R}$は数の大小により全順序集合
- $X$は最大元を持つ$\Rightarrow$最大元と上限は一致する
- $X$は最小元を持つ$\Rightarrow$最小元と下限は一致する
証明は、最大最小を$X$とその上界下界について考えればよいです。
この命題から、上限下限は元の範囲の最大最小の要素を持っていることになります。
おわりに
今回挙げた上限と下限なんですが、実は解析学以外であまりみないんですよね。実数の連続性で存在が保証されない一般の集合では、扱いが難しいのかもしれません。そのせいで直感的な例が数列しか思いつきませんでした。他には、束($lattice$)と言う順序関係による代数的構造があり、これは上限下限を用いて定義されますが、代数構造を説明するための道具が足りないので今回は省きました。
次回は、名前だけやたらと有名になった「写像」を取り扱います。
以上、ケンけんでした。

