こんにちは!ケンけんです。前回は大小関係の一般化「順序関係」を定めました。
今回は、最大最小の一般化「最大限・最小限」と重要な情報「極大元・極小元」を考えます。
キーワード:最大最小・極大極小
$\mathbb{R}$:実数全体の集合
導入
前回大小関係の中で、最大値・最小値が存在する場合を導入の際に見ました。
例えば、$\mathbb{R}$上「$2\leq x \leq 4$」とすると、$x$では最大値$4$、最小値$2$となりました。

例:$2\leq x \leq 4$での$x$の範囲の図
$\mathbb{R}$は全順序集合なので,$2\leq x \leq 4$に対して次のことが言えます。
- $(a \leq 2) \Rightarrow (a \leq x)$
- $(4 \leq a) \Rightarrow (x \leq a)$
まずは、この最大値・最小値を全順序集合である$\mathbb{R}$から半順序集合にまで拡張したいです。その例としては、半順序集合であったべき集合(部分集合間の包含関係)を考えます。

例:$X=\{1,2,3\}$のべき集合の樹形図
上の図は、一見左端が$\{1\}$と$\emptyset$で枝分かれしているように見えます。しかし、空集合はすべての集合の部分集合より$X$を普遍集合と見ると$\emptyset \subset \{1\}$となります。
そして$X$の部分集合$Y$について$X \subset Y$となります。
従って、$X=\{1,2,3\}$についてべき集合$2^{X}$は、包含関係について
- $\emptyset$が最小の元
- $X$が最大の元
と思うことができます。しかし、このべき集合の部分集合を考えるとうまくいかなくなります。
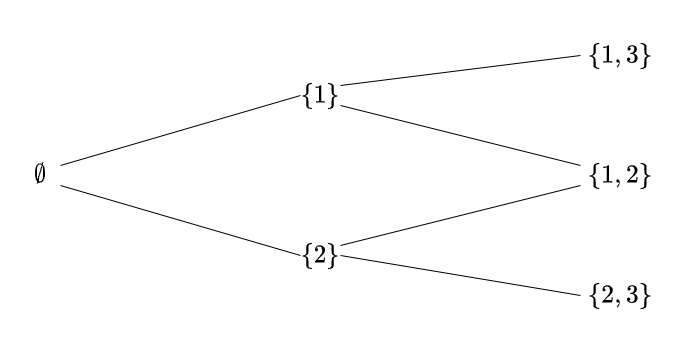
例:$Y=\{\emptyset ,\{1\} ,\{2\} ,\{1,2\} ,\{1,3\} ,\{2,3\} \} \subset 2^{X}$の包含関係の図
このとき、包含関係で最も右側にあるのは$\{1,2\} ,\{1,3\} ,\{2,3\}$の3つですが、互いに包含関係がないのでどれも最大の元だとは言えません。つまり、最大の元を持つ集合でもその部分集合が最大の元を持つとは限らないことがわかります。
逆に、最小の元は空集合$\emptyset$を持っているので常に存在します。しかし、右端の集合は一つの枝だけに注目して一列で見ると最大の元であることは言えます。(例:$\emptyset \subset \{1\} \subset \{1,3\}$)ここから、$\{1,2\} ,\{1,3\} ,\{2,3\}$は最大の元らしき情報を持っていると言ってもよいことになります。そこで出てくるのが元の極大・極小です。
これらの言葉は高校数学で見聞きしたことがあります。それは微分法の応用で、極大値を求めて最大値を答えると言った問題です。数学Ⅱですね。例えば次のような関数を考えます。

例:関数$f(x)=-x^4+2x^3-x^2$のグラフ(関数グラフソフト「GRAPES」利用)
上の図は、グラフ描写ソフトで書いているので既に関数のグラフが既にわかっています。なので、グラフから最大値は$x=0,1$で$0$、最小値は存在しないとすぐにわかります。しかし、数学Ⅱの知識では上のグラフの概形を正確に書くことはできません。なぜなら2回微分を必要としており数学Ⅲの内容だからです。このときに使ったのが極大値・極小値でした。
| $x$ | $\ldots$ | $0$ | $\ldots$ | $\frac{1}{2}$ | $\ldots$ | $1$ | $\ldots$ |
| $f'(x)$ | $+$ | $0$ | $-$ | $0$ | $+$ | $0$ | $-$ |
| $f(x)$ | $\nearrow$ | $0$ | $\searrow$ | $-\frac{1}{16}$ | $\nearrow$ | $0$ | $\searrow$ |
表:$f(x)=-x^4+2x^3-x^2$の増減表
$f'(x)=0$となる$x$で$f(x)$は極値をとり、その点の前後での$f'(x)$の正負から$\nearrow,\nwarrow$が決まります。そして、増減表から極値で最大最小が判定できグラフを書かずに考えることができました。
このとき、$x=0,1$で極大値$0$を取ることがわかり増減表から最大値だと言えます。極小値として$x=\frac{1}{2}$で$f(\frac{1}{2})=\frac{1}{16}$がありましたが、関数自体が負の値をいくらでも取れるため最小値ではありませんでした。
では、関数の定義域を$0 \leq x \leq 1$に制限するとどうなるでしょう。このとき、増減表の「$x \leq 0$」と「$1 \leq x$」の部分が無くなるため極大値・極小値をそのままです。そうすると、最小値でない極小値$f(\frac{1}{2})$が最小値になります。
この範囲の制限、部分集合を取ることに似ていますね。
$Y=\{\emptyset ,\{1\} ,\{2\} ,\{1,2\} ,\{1,3\} ,\{2,3\} \} \subset 2^{X}$の例では、$\{1,2\} ,\{1,3\} ,\{2,3\}$が包含関係で右端になる部分集合でした。$2^{X}$は半順序集合なので、増減表のようなことはできません。なので、極値の意味をそのままでは使えず言いかえが必要です。
極値の意味は、極値点の前後では$f'(x)$の正負が入れ替わるためグラフを書けなくても、
山($\frown$)か谷($\smile$)のイメージできます。
つまり、次のように説明できます。
$$極値となる点aの周辺(十分小さなh>0でa-h<x<a+hの範囲)で、最大または最小$$
適切な部分集合$Z=\{\emptyset , \{1\} , \{1,3\} \}$を取ると、$\{1,3\}$は$Z$での最大の元となりました。
従って、$\{1,3\}$は$Y$の極大の元だと説明できます。
このように解釈すれば、関数の極大値・極小値から順序関係での極大・極小を説明できそうです。
極大極小の定義に向かって
最後に、極大極小は最大最小の条件を考えます。
最大最小は、半順序集合$(X,\leq )$について論理式でキレイに書けます。
- $a$は最大 $\iff \forall x \in X(x \leq a)$
- $a$は最小 $\iff \forall x \in X(a \leq x)$
極大極小は、大小関係がある元だけで考えると最大最小でした。これは言い換えると、「より大きい元」・「より小さい元」が存在しないことを意味します。
例えば、集合$X$について$x \in X$が上の意味で極大の元とします。このとき、$x$を最大の元とする$Y \subset X$を考えます。今、$x \leq y$とするような$y \in X$が取れる場合は、$Y’=Y \cup \{y\}$とすることで最大の元を$y$とする部分集合が作れます。これによって、新しく極大元$y$が取れます。しかし、これを許してしまうと次の操作ですべての元が極大元というトンチンカンなことになります。
- $x \in X$について「\{x\}ではxが最大の元$」より$x$は極大の元
- $x \leq y$とする$y \in X$について「\{x,y\}ではyが最大の元$」より$y$は極大の元
では、どうすれば解消できるでしょう。それは、最大最小が極大極小であることで解決されます。
最大の元$x \in X$について、ある元$y\in X$で「$x \leq y$」となってはいけませんね。つまり、それを満たさない上の状況は問題になります。なので次のように説明して回避します。
$$xは極大の元 \iff \forall y \in X((x \leq y)\Rightarrow (x=y))$$
つまり、極大の元$x$について「$x \leq y$」となる元$y$が取れた場合には、それは極大元そのものとなることです。これにより、先ほどのようなすべての元が極大元となるようなことはなくなり、最大最小に話を制限しても矛盾しなくなりました。
最大最小・極大極小
それでは定義していきます。
$U$:普遍集合 $X \subset U$
$(X \leq )$:半順序集合 $a \in X$
- $a$は最大元($\rm{maximum \; element}$) $\overset{def}{\iff} \forall x \in X(x \leq a)$
- $a$は最小元($\rm{minimum \; element}$) $\overset{def}{\iff} \forall x \in X(a \leq x)$
- $a$は極大元($\rm{maximal \; element}$) $\overset{def}{\iff} \forall x \in X((a \leq x) \Rightarrow (x=a))$
- $a$は極小元($\rm{miminul \; element}$) $\overset{def}{\iff} \forall x \in X((x \leq a) \Rightarrow (x=a))$
最大最小は、実数での最大値・最小値と同じようになっています。
また、極大極小を上で議論したように論理式で書けました。
論理式から、「最大元(または最小元)$\Rightarrow$ 極大元(または極小元)」であることもわかります。
実数で極大値や極小値が出てこなかったのは、$\mathbb{R}$が全順序集合だからです。極大極小は、2つ以上の順序関係による樹形図で最も右側に現れるときに登場します。従って、すべての元が一列で並ぶ全順序集合では極大元が存在する場合、定義からそれが最大値であることを意味します。だから、これまでは必要なかったのです。しかし、半順序集合まで話を広げると包含関係などで一列に並べられない場合があるので極大元ができてしまうのです。
また、半順序集合の場合、極大元が存在しても最大元が存在するとは限りません。それは、樹形図の枝分かれを考えると、すべての元で比較できないときは定義を満たす元が存在しないからです。
こんなところでも全順序集合と半順序集合の差がわかります。
おわりに
数学では、意外と最大最小は解析学(微積分)以外ではあまり登場せず、極大極小の方が頻繁に出てきます。これは、半順序集合の特定の部分集合の中だけで最大最小らしきものが必要になることが多いからだと思われます。また、極大極小について「超える元・超えない元」というものが非常に分類がしやすいことも利用される理由でしょう。
次回は、順序関係の「上界・下界」とその最大最小である「上限・下限」を取り上げます。
以上、ケンけんでした。

