こんにちは!ケンけんです。前回は、等号の一般化である同値関係を取り上げました。
今回は、数の大小関係の正体である順序関係を取り扱います。
キーワード:順序関係
導入
スタートはやっぱり数の大小関係です。
$\mathbb{Z}$:整数全体の集合
- $2 \leq 10$だが$4\leq -4$は誤りである。
- $a<b,c<d$のとき、$a+c<b+d$が成り立つ。
- $a<b$のとき$\frac{1}{b} < \frac{1}{a}$が成り立つ。(逆数の大小)
- $2\leq x \leq 4$について、$x$は$2$で最小値、$4$で最大値である。
自然数が数えられることを延長し、実数が数直線に表せることで説明されることが多いです。

例:数直線と$2\leq x \leq 4$での$x$の範囲の図
大小関係は、四則演算や逆数などの性質がありました。
数の最大・最小は大小関係において最も大きな数・最も小さな数として与えられます。
また、2つの数$x,y$(実数まで)は必ず「$x<y$」、「$x=y$」、「$x>y$」、のいずれか一つだけ成り立ちます。これは、実数が数直線としてすべて一列に並べられる事実から、より右側(正の方向)に位置する実数の方が大きいと判定できます。
「$\leq$」以外にも不等号として「$>$」と「$<$」があります。「$\leq$(以上・以下)」は、「$=$」になる場合も含んでいて、「$<$(より小さい・大きい)」は等号にならない大小関係を表しています。
さて、大小関係は2つの数を比較した結果なのでこれは2項関係になっています。
今回は、等号から必要な情報を抜き出して同値関係を構成したように、大小関係にも必要な情報が存在するはずです。そこで集合の情報だけで得られる事実を考えてみましょう。
上で挙げた例では、
- 四則演算や逆数について
- 最大・最小が取れること
- 必ず大小または等しい
の3つがありました。
まず、四則演算はまだ定義する言葉がなく、これまでの議論で登場していないので必要ないでしょう。
次に、最大・最小についてですがこれも必要ありません。なぜなら、数の大小関係でも存在しない場合があるからです。例えば、$0<x<1$について最大値も最小値も「これだ!」と決められません。数直線上に範囲にを書くときに、斜め線と○で描いていた状況です。

例:$2<x<4$での$x$の範囲の図
このように範囲が閉じているように見えても「より大きい」場合、最大最小は考えられません。
しかし、この範囲内の数も数直線から大小は必ず決まります。ここから、最大最小も大小を説明する上では必ずしも必要とはならないです。
最後に、大小が必ず決まることですがこれは今の段階では必要かは考えられません。
なぜなら、数の他に大小関係をまだ知らないからです。
数以外の大小関係の例
というわけで、他の大小関係を考える必要があります。数以外で今知っている対象には、集合があります。それで大小を考えてみましょう。集合を数の代わりに見るのは、部分集合を元と見る「べき集合」がありました。この場合が、イメージしやすいのでこれで考えます。
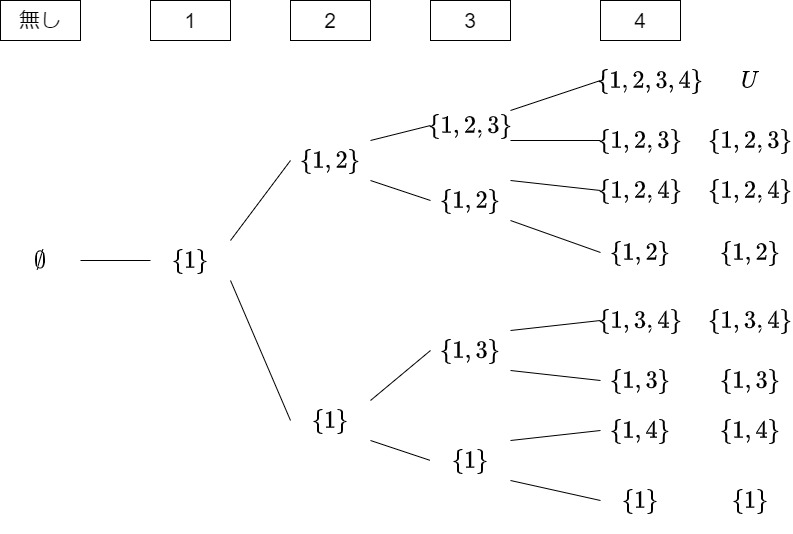
例:集合$U=\{1,2,3,4\}$での部分集合の一部
上の図は、以前べき集合を導入するときに使ったものです。その時に、右側へ行くほど集合間の棒線が「$\subset$」の関係があることに触れていました。この考え方、数直線に少し似ていますね。また、部分集合は2つの集合の間の関係であり集合の一致の説明に使われました。
$$X=Y \iff (X \subset Y)\wedge(X \supset Y) (X,Y;集合)$$
これは、数の不等号でも同じことが言えます。
$$x=y \iff (x \leq y) \wedge (x \geq y) (x,y\in \mathbb{R})$$
2つの数式が一致することを示す時に、この不等号を調べる方法がありました。情報が、不等号と部分集合でほとんど同じであることがわかります。
さて、「$\subset$」を集合での大小関係と見れることがわかりました。ここから数との違いを見ていきます。そうすると、2つの集合の間に必ずしも大小関係があるとは限らないことがわかります。
上の図にて、$\{1,2\}$と$\{1,3\}$の間には部分集合の関係がないことがわかります。
以上から、必ずしも2つの元で大小が決まる必要もなさそうです。
では、何をもって大小関係を決めればよいのでしょう。
大小がわからない場合が問題になるため、比較できるものだけで大小関係を考えれば十分そうです。
$U$を普遍集合、$X \subset U$とします。
まず、数とべき集合のケースで類似した性質がありました。それは、双方向の大小関係がある場合に一致していること言うことです。論理記号で書くと次のようになります。
- $x,y \in X=\mathbb{R}$のとき、$(x=y) \iff (x \leq y)\wedge (x \geq y)$
- $A,B \subset X$のとき、$(A=B) \iff (A \subset B) \wedge (A \supset B)$
これは、2つの異なる大小関係で共通するため定義に加えてよいでしょう。
次に、大小関係の推移律を考えます。数の大小・部分集合ともに推移律を満たします。
- $x,y,z \in X=\mathbb{R}$のとき、$(x\leq y) \wedge (y \leq z) \Rightarrow (x \leq z)$
- $A,B,C \subset X$のとき、$(A\subset B) \wedge (B \subset C) \Rightarrow (A \subset C)$
同値関係でも登場した推移律ですが、2つの関係があると両端を結んで考えていいと言う強力な道具です。3つ以上の元を考えるときには、2つの状況にして考えればいいのです。
同値関係で存在した反射律「$x=x$」はどうでしょう。「$<$」ならば自分自身が一致するので当然成り立ちません。しかし、「$x<y$」は「$x \leq y$」であり「$x \neq y$」であることを意味していました。つまり、「$<$」は「大小関係$(x \leq y)$」と「元の一致$(x=y)$」で決まるため、大小関係として準備するのは「$\leq$」だけで十分です。
等号を許せる「$\leq$」ならば反射律「$x\leq x$」も成り立つと言っていいでしょう。
最後に、同値関係で存在した対称律は明らかに成り立ちません。例で挙げたように、「$-4 \leq 4$」は正しいですが「$4 \leq -4$」は誤りです。大小関係の一般化を考えるのに、具体的対象の数の大小で成り立たないのでは意味がありません。従って、対称律は成り立ちません。
以上から、大小関係を指定するのは「反射律」「推移律」、そして大小から等号を導く「反対称律」の3つが大小関係を意味するために必要なのだと思えそうです。
順序関係
それでは、定義しましょう。
$U$:普遍集合 $X \subset U$ $x,y,z \in X$
$\leq$:$X$の元についての2項関係
- $x \leq x$
- $(x \leq y) \wedge (y \leq z) \Rightarrow x \leq z$
- $(x \leq y) \wedge (x \geq y) \Rightarrow x=y$
$\leq$は$X$の順序関係 $\overset{def}{\iff} 1. 2. 3.は真$
($order relation$)
$X$は半順序集合($partially ordered set$)
$(X,\leq)$と書く。
$x<y \overset{def}{\iff}(x \leq y) \wedge (x \neq y)$
同値関係から引き続き「1.反射律」、「2.推移律」となります。
そして3.が順序関係独特の、「反対称律」です。
それぞれの意味は導入の際に考えたので細かい点は省略します。
「$<$」は、論理式で「順序関係を持つ」ことと、「元として一致」しないことで説明されます。
言葉の中では、部分集合による集合間の関係を包含関係と呼ぶことがあります。
きれいな順序 全順序
導入の例2つの明確な差で、2つの元を取ると順序により比較できるかがありました。
実数は数直線なる「一列に並べました」と言わんばかりのものまで存在します。対してべき集合の例では一つの元からなる集合は、元が一致しないと包含が存在せず比較できませんでした。(例:$x \neq y$のときは$\{x\}$と$\{y\}$は比較できない)
ここから、順序関係にはより強い条件として、比較可能であることを貸してもよさそうです。
$U$:普遍集合 $X \subset U$
$(X, \leq)$:半順序集合
$(X, \leq)$:全順序集合 $\iff \forall x,y \in X((x\ \leq y) \vee (x \geq y))$
($totally ordered set$)
数の大小では、「$<$」「$=$」「$>$」のいずれかに決まるとありました。しかし、順序関係に反対称律を認めているため、双方向の順序関係「$\leq ,\geq$」が成り立つときには自然と「$=$」が決まります。「$<$」と「$>$」は等号が成り立たない場合であり、反対称律の対偶を取ればどちらかの不等号が成り立たない場合であることがわかります。
$P,Q$:命題
$(P \Rightarrow Q) \iff ((\neg Q) \Rightarrow (\neg P))$:(対偶)
つまり、「$\neq$」は次のように説明されます。
$$x \neq y \Rightarrow (x \nleq y) \vee (x \ngeq y)$$
全順序集合の定義は2つの元が必ず比較できることだったので、少なくとも一方の不等号が成り立ちます。従って、もう一方に不等号が成り立たないことを意味します。
そして、「$<$」は「$\leq$」かつ「$\neq$」でした。既に、「$\neq$」を仮定しているため、「$\ngeq$」ならば説明できます。従って、全順序集合ならば、「$<$」「$=$」「$>$」のいずれか一つに決まり、数の大小関係3通りに復元できます。
例としては、当然実数までの数がありますが、包含関係でも全順序集合を作ることができます。
$X=\{a,b,c\}$:集合
$Y=\{ \emptyset , \{a\} , \{a,b\} , X\}\subset 2^{X}$
このとき、$(Y,\subset)$は全順序集合である。
これは包含関係により一列に並べることができます。
$$\emptyset \subset \{a\} \subset \{a,b\} \subset X$$
これは、すべての実数が一列に並べられることに似ています。全順序集合の元は形は違えど一列に並べられることになります。半順序集合の場合は、べき集合の例からわかるように途中で枝分かれしてしまいます。このせいで直接包含関係があるか考えられないと言えます。
図式的にイメージしやすいですね。
- 全順序:すべての元を一列に並べられる。
- 半順序:順序関係で図を作ると枝分かれする場所がある。
おわりに
直積の時に登場した座標平面と関数のグラフは、実数全体が全順序集合であることを利用しています。つまり、数以外でも全順序集合ならばグラフのような集合の表示が可能になります。こんな風に見ると、座標平面とグラフには結構な情報が詰まっているとわかると思います。
次回は、順序集合の元が最大・最小、そして極大・極小であることを扱います。
以上、ケンけんでした。
べき集合についての記事