こんにちは!ケンけんです。前回は、「元を含む」の真偽からべき集合というこれまでと違った集合を定義しました。
今回は、集合の構成として最後の対象「直積集合」を取り扱います。
キーワード:直積集合
導入
高校数学までで、関数や図形を考えるときに縦と横に軸を取り座標平面上で考える方法がありました。そのうえで、関数を考えると以下のように図示できます。
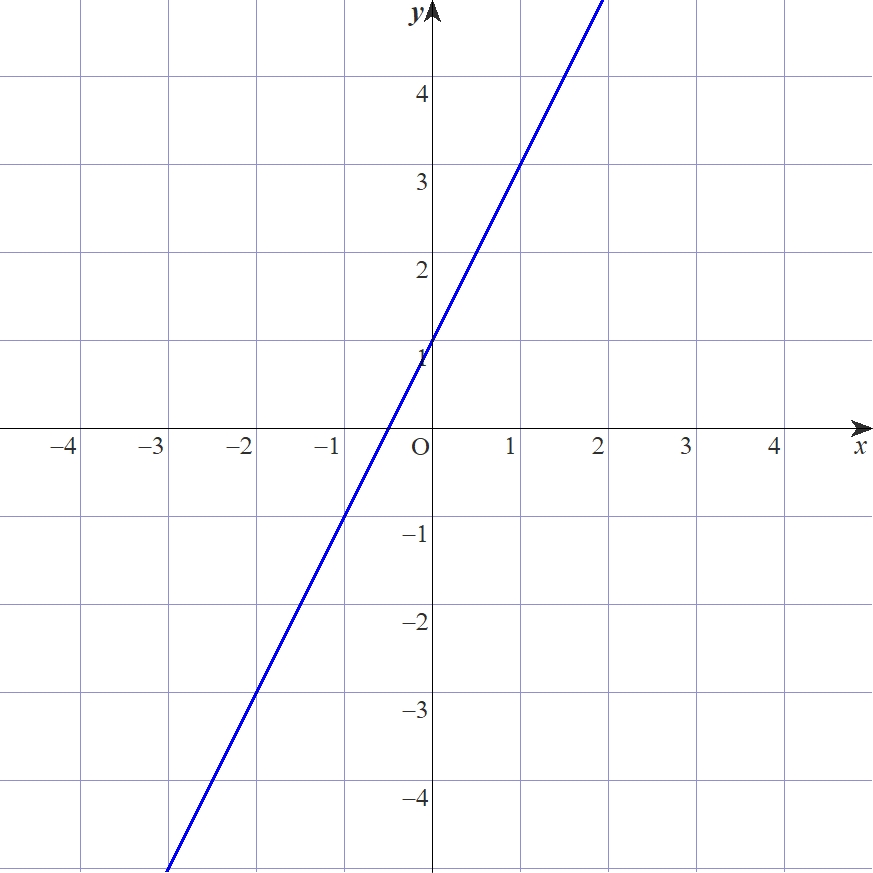
例:座標平面と直線$l:2x-y+1=0$のグラフ
座標平面は、縦と横に軸を平面に取ったもので4つの象限に分けられます。そして、関数や方程式によって定まる図形(例は直線)は「$x$に対しての$y$を結ぶ(関数)」または「方程式を満たす組$(x,y)$を結ぶ」ことで描けるのでした。
座標平面上では、どこに点を打っても必ず$x$座標と$y$座標が一つに決まります。また直線$l$上の点$(x,y)$は、すべて「$2x-y+1=0$」を満たす座標平面上の点です。
なので、次のように言えるでしょう。
- 座標平面:座標$(x,y)$を元とする集合
- $l$のグラフ:$l$の式を満たす座標の集合
実数全体の集合は$\mathbb{R}$と書きます。集合の定義に従うと、座標平面は点$(x,y)$を元と見て$$\mathbb{R}^2=\{(x,y)|x,y \in \mathbb{R}\}$$のように書くことができます。ここから、座標平面は2つの集合$\mathbb{R}$を使って定義される集合だと言うことができます。
2つの集合から作られる集合として共通部分と和集合がありました。この2つとの違いは、元定義の述語が「かつ」、「または」により作られていますが、元は元の集合の元でした。座標平面は、$\mathbb{R}$の2つの元から決まる元を持つ集合のため異なるものだとわかります。
次に、直線$2x-y+1=0$を考えます。直線上の点は、$\mathbb{R}^2$の条件を満たす点を結んでできる図形なので、$\mathbb{R}^2$の部分集合と言えます。なので、次のように集合で書けると言えます。
$$L=\{(x,y) \in \mathbb{R}^2|2x-y+1=0\}$$
直線に見える図形は、「$2x-y+1=0$」を満たす点$(x,y)$の集合と説明できます。
では、$\mathbb{R}$の代わりに$\mathbb{C}$(複素数全体の集合)に置き換えるとどうなるでしょう。$\mathbb{C}$は座標平面の代わりに、実軸・虚軸による複素平面を考えていました。これは、座標平面の縦軸・横軸を置き換えたもので、実質同じように扱えるのでした。$\mathbb{C}$には、一般の大小関係がないため数直線を書くことができません。なので、$\mathbb{C}^2$のような集合は考えることはできない!というわけではありません。
確かに、この座標平面上の点の集合として$\mathbb{R}^2$を書きました。しかし、その集合の定義に大小関係の述語が存在しません。あくまで、$\mathbb{R}$の元2つからなる元としか指定しておらず、座標平面で書けるのは実数の性質として別口でついてきたものです。実数がたまたま並べられるから、座標平面上の点を指定するだけで集合が座標平面を復元できるのです。
なので、集合の定義として倣うならば次のように$\mathbb{C}^2$を考えられます。$$\mathbb{C}^2=\{(z,w)|z,w \in \mathbb{C}\}$$
さらに、座標平面は縦軸・横軸が実数でしたが、$\mathbb{C}^2$のように図示にこだわる必要がありません。つまり、数のように次のような書き方をしてみます。$$\mathbb{C}^2= \mathbb{C} \times \mathbb{C}$$この書き方から、左右がともに$\mathbb{C}$である必要はなく異なる2つの集合で同じことが考えられます。例えば、次のような集合を考えることもできます。
$$\mathbb{Q} \times \mathbb{R}=\{(q,x)|(q \in \mathbb{Q}) \wedge (x \in \mathbb{R})\}$$
他には有理数の構成で使われるものがあります。有理数$r= \frac{p}{q}$は、分母を自然数(正の整数とします。)、分子を整数とみなすことで説明できます。従って、構成するときに次の集合を考えることができます。
$$\mathbb{Z} \times \mathbb{N}=\{(z,n)| (z \in \mathbb{Z}) \wedge (n \in \mathbb{N})\}$$
実際には、ここに追加の情報が必要ですが、有理数を作るときに異なる集合で「$\times$」を考えることが必要になります。
この2つの集合の元で決まる元からなる集合を一般に直積集合と呼びます。
直積集合
それでは、定義していきます。
$U$:普遍集合 $X,Y \subset U$
$X \times Y=\{(x,y)|(x \in X) \wedge (y \in Y)\}$
$X \times Y$:$X$と$Y$の直積集合
($direct$ $product$)
$(x,y) \in X \times Y$に対し次のように呼ぶ。
- $x$:$X$の成分
- $y$:$Y$の成分
共通部分と異なる部分は、2つの元$x,y \in U$について「かつ」を考えているところです。
また、組み合わせを考えると、直積集合の元の取り方が元々の集合より多くなります。
導入でもふれたように、$X,Y$の元に大小関係の間に何も構造(四則演算や大小関係など)が必要ないことが定義の述語部分からわかるでしょう。つまり、直積集合は最も自由な状態でこの中に情報を追加することで様々な対象に変わっていきます。
例
さて、直積集合を定義できましたが高校数学では、座標平面や関数のグラフを集合の言葉で書いていません。実は、座標平面以外で直積集合を暗に使って記述したものがあります。それが、「方程式の解」です。
例えば、次の連立方程式を考えます。
$$\begin{cases} \begin{eqnarray} 2x+y=1 \\ 4x+7y=7 \end{eqnarray} \end{cases}$$
このとき、解は「$x=0,y=1$」です。別の書き方で、「$(x,y)=(0,1)$」という方法がありました。これは、暗に方程式の解が「$\mathbb{C}^2$」の元であることを使っています。
他には、数学Ⅰでの2変数関数の最大値問題(平方完成により解ける問題)があります。このとき、「$(x,y)=(a,b)$で最大値○○を取る。」と書いている場合があります。
ただし、高校ではあまり集合を使いたくないのか「$x=a,y=b$のとき最大値○○」と書き下す方法が主流です。
大学数学で初めに現れる直積集合は、おそらくベクトルだと思います。
今では数学Cに移動しましたが、以前は数学Bだったので多くの方が知っているでしょう。ベクトルは、長さと向きの情報を持つ「量」でした。その中で位置ベクトルは、座標平面のように成分で書くことができました。そして、向きの情報が位置ベクトルによる表示から説明できるため、「$(x,y)$」の形の元とその計算規則によりベクトルを定義します。そして、その成分が実数から離れて複素数などの順序の存在しない元へ拡張されていきます。その空間をベクトル空間と呼びます。
特に、「$\mathbb{R}^2$」や「$\mathbb{C}^2$」の形の集合を数ベクトル空間と呼びます。
線形代数学では、まず数ベクトル空間を学ぶところから始まります。その中で、直積集合を何度も使うことになるでしょう。
おわりに
直積集合は、今後様々や場所で登場するひときわ異質な集合です。例でグラフをあげたように、関数を定義する場合に用いられたり、四則演算を定義するときにも使われます。関数については今後近いうちに見ていくことになると思います。
次回は、述語の二項関係から集合での「関係」と「同値関係」を扱います。
以上、ケンけんでした。