こんにちは!ケンけんです。前回は空集合を命題論理の視点から形式化しました。
今回は、部分集合の集まり「べき集合」を取り上げます。
キーワード:べき集合
導入
確率の題材として、コイントスがあります。これは、裏表の出る確率が(同様に確かな場合)2分の1であるケースです。このとき、$$コイントスで4回中裏が3回出る確率$$といった問題があります。これは、4回中1回だけ表が出ればよいので次のようになります。$$ _{4}C_{1}(\frac{1}{2}) (\frac{1}{2})^3=\frac{1}{4}$$では、なぜこの式で確率が求まるのでしょう。本来確率は、全事象($2^4$通り)の中で考えている事象(4回中1回だけ表の通り数)の割合でした。従って、普通は考えている事象が何通りかを数える必要があります。そこを、組み合わせ($\ _{n}C_{r}$)で説明できるため手間を省いているのでした。
では、組み合わせを使わない場合どんな道具を使って数え上げていたでしょう。もちろん上の例は、たかが16通りなのですべて箇条書きにしてもいいですが、場合分けの容量で考える「樹形図」というものを学んだと思います。
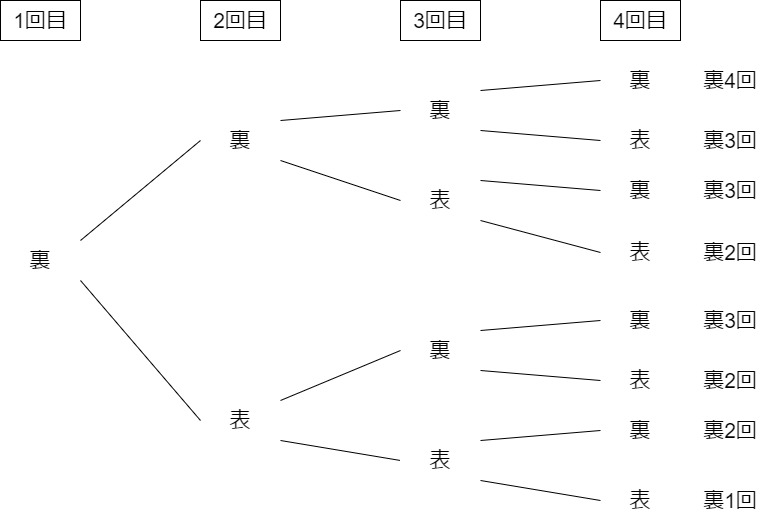
例:4回コイントスを行う場合の樹形図の一部
このように枝分かれのように描き、最終的に右端が事象となるように描きます。この右端の情報で組み合わせが決まっており、組み合わせの式が定義できるのでした。
コイントスは、確率統計では2項モデルと呼ばれ単純なタイプです。金利計算でも、○○円儲かる・損すると設定して最終的な儲けの予測を行います。(実際にはここまで単純ではないです。)
で、この裏表の2通りで作られる情報を私たちは既に扱ってませんか。そう、「命題論理」とそれに従う「元が集合に属す・属さない」です。
今回題材となっているべき集合とは、裏表を「$x$は○○の元」と「$x$は○○の元ではない」として見たものです。確率では右端に注目したことと同様に、べき集合も右端の情報が元に反映されます。では、樹形樹中の「回数」と「裏・表」は何が該当するのでしょう。
これは全体集合$U$に対して、次のように言いかえられます。
- $コイントスの回数 \iff $U$の元$
- $裏・表 \iff $U$の元を含む・含まない$
例えば、$U=\{1,2,3,4\}$について
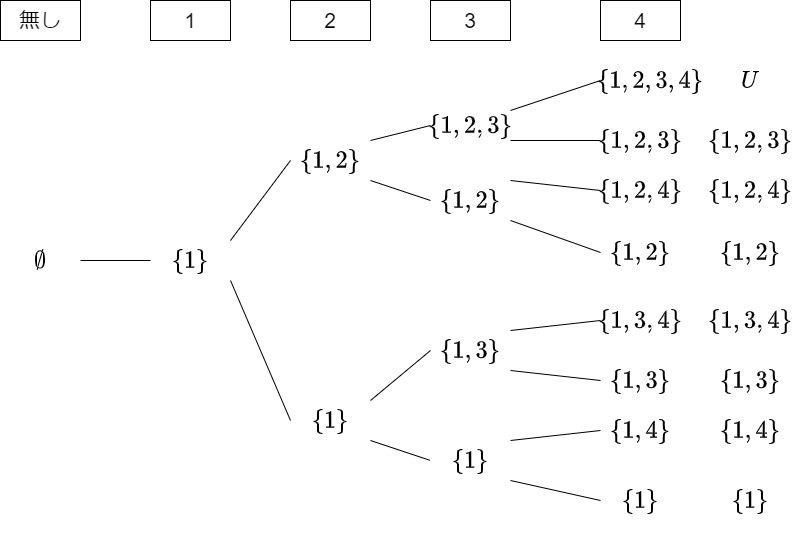
例:$U=\{1,2,3,4\}$の樹形図の一部
確率では、全事象は右端の結果でした。全事象は考えられる事象すべての集合と言えます。
それにならうと、$U=\{1,2,3,4\}$の例では$U$の部分集合全体の集合となります。これがべき集合と呼ばれる新しい集合です。そして、樹形図は左の空集合から始まり左へ進むほど部分集合として含まれる形に広がっていきます。
この例では、全体集合$U$のべき集合となっています。もちろん「$U= \mathbb{Z},X=\{1,2,3,4\}$」とした場合には、$X$のべき集合を考えることができます。
ただし、何度も言った通り集合の元は書き下せるとは限りません。従って、上のような図を描けない場合がほとんどです。なので、この樹形図で得た情報として「考える集合の部分集合を元とする」性質で定義します。
べき集合
それでは定義していきます。
$U$:普遍集合 $X \subset U$
$2^{X}=\{Y \subset U| Y \subset X\}$
$2^{X}$:$X$のべき集合($power set$)
書き方で、なぜ$2^{X}$なのかと言うと「$x \in 2^{X}$」または「$x \notin 2^{X}$」の2通りが$X$の元すべてに考えられるからです。仮に$X$が$n$個の元を持つ集合なら、$X$の部分集合の取り方は$2^n$個です。コイントスの全事象を求めることと全く同じです。
元が書き下せない集合($\mathbb{Q}$など)の場合、この手法は使えませんが元の取り方が2通りずつである特徴を持っているためこの書き方になっていると言えます。
他の書き方で、英語の頭文字から「$\mathcal{P}(X)$」と書く場合もあります。
このべき集合は、元が集合になっています。そのため、言語化すると「集合の集合」と2重表現のようになっています。そこで、混同しないように「集合族($family of sets$)」と呼びます。この「族」は、新しい対象ではなく混同を避けるための言葉なので注意してください。
べき集合の行き先
さて、べき集合を定義したはいいけれど何に使うかがはっきりしていません。導入の確率論では、有限個の通りと有限回の操作による事象だったため、次のように確率を言い換えられるでしょう。
$$\frac{考える事象の総数}{全事象}=\frac{対象の部分集合の数}{元の集合の元の数}$$
高校までの確率論は、高々数えられる状況のみですべて集合の元の数として言い換えられます。
しかし、書き下せない事象数の場合や、操作回数が無限回などを考えるようになると上の例はもはや意味がありません。数えられないものや無限回操作を人間は認識できないからです。
では他に何かで使えないかと言うと、数学の中なら「位相」だと思います。
位相とは、2点間の距離$d(x,y)=\sqrt{x^2-y^2}$の一般化で、集合に距離(近さ・遠さ)のような構造を作りたい場合に使用されます。そしてこの定義で、「開集合系」と「位相空間」という言葉が出てきます。「開集合系」とは、開集合と呼ばれる集合の族でべき集合の部分集合となります。
集合$X$について、2つの言葉は次のように説明できます。
- 開集合系$\mathcal{O}$:$X$の元の間の定規
- 位相空間$X$:近さ構造$\mathcal{O}$を持つ集合
位相(部分集合の族)の取り方によって、集合の中での近さの尺度が全く変わります。
もし、べき集合が「開集合系」であるときは、単純な位相になります。近さを決める尺度(物差し)が一番細かく設定されているからです。このべき集合で位相を設定すると次の距離と同じ「近さ」の構造を持つことがわかります。
$$d_{\infty}(x,y)= \begin{cases} 0 & x=y \\ 1 & x \neq y \end{cases}$$
これは、距離の中でも離散距離と呼ばれる距離の一つです。元を数え切れる集合の場合、2つの異なる点の距離がすべて1であることから点を長さ1の棒で結んだ図形のようになっています。べき集合による位相は、この離散距離による「近さ」の定義と同じものだと位相空間論では説明できます。
べき集合による位相を、距離の言葉に倣って「離散位相」と呼びます。
位相は近さの他に、先ほどの数え上げられない場合や「無限」回の操作などを説明する場合に登場します。ですが、今回は利用の例として取り上げただけなので、これ以上深いりはしません。
おわりに
今回の記事を書くにあたって、べき集合のことをいろいろ調べましたが想像していたよりもべき集合の応用先が少なかったです。位相以外にブール代数(真偽で考える代数)などにも利用されるようです。ですが、一般数学で広く使われているのは位相だと思うため、今回は採用しました。
次回は、集合のタイプで重要な「直積集合」を取り扱います。
以上、ケンけんでした。

