NST-10：論理で集合を作る

こんにちは！ケンけんです。前回は集合の一致（$=$）について調べました。

今回は、集合が述語（命題）論理に従って情報を持つことを見ていきます。

キーワード；補集合、部分集合、和集合、共通部分

導入

命題論理では、「否定（$\neg$）」、「ならば（$\Rightarrow$）」、「かつ（$\wedge$）」、「または（$\vee$）」の4つが2つの命題をつなぐ道具として登場しました。述語でも同様に使えます。

そして集合は$$\{x|P(x)\}$$のような表記で表され、この集合の元$x$は命題$P(x)$を真にするものの集まりでした。つまり、条件部分の命題$P(x)$に少し手を加えることで新しい集合を考えることができます。

述語$P(x),Q(x)$について集合$X = \{x | P(x)\},Y=\{x | Q(x)\}$を取ります。このとき、

• $\{x | \neg P(x)\}$
• $\{x | P(x) \wedge Q(x) \}$
• $\{x |P(x) \vee Q(x)\}$
• $\forall x(P(x) \Rightarrow Q(x)) \iff \forall x((x \in X ) \Rightarrow (x \in Y))$

といった$X,Y$から4つの「新しい集合」と1つの「$X,Y$間の元のならば（$\Rightarrow$）」が考えられます。

ちなみに、4つ目の元の関係は前回の集合の一致の「$\Rightarrow$」が成り立つが、「$\Leftarrow$」がわからない弱い形になっています。なので、今から定義する言葉で集合の一致の語り方を言い換えることもできます。

集合の構成

今回はこれまでの命題と集合の言葉で定義するだけなので早速見ていきましょう。

これらは高校での集合で既に登場しており、定義自体は日本語で書かれた場合とさほど変わらなく感じるかの知れません。ですが、これまで「書き下せない」または「数えられない」元からなる集合を考えられるようにすることが必要だと伝えてきました。従って、「～の元」などの言葉ではなく述語のような「性質」だけで説明できることが大切です。

導入でも取り上げたように、部分集合が前回の集合の一致での定義の一方向のみがわかっていることが定義であるとわかります。従って、集合の一致（$X=Y$）は述語ではなく今定義した集合の言葉で書くと、$$X=Y \iff (X \subset Y) \wedge (X \supset Y)$$と言い換えることができます。（命題　NST-5-6 9.を用いる）

命題論理と集合の記号は、($\Rightarrow と \subset$)、（$\iff と \=$）、（$\wedge と \cap$）、（$\veeと \cup$）で関連しています。従って、集合記号は命題論理に情報（元）を上からかぶせた形になっているとわかります。

高校では、集合を可視化する道具として「ベン図（$Venn　diagram$）」を用いました。これは集合を一つの円（または楕円など）で表し、集合間の重なりなどを理解する助けとなります。以下の4つの図で塗りつぶされている部分はそれぞれ補集合・共通部分・和集合・部分集合を表しています。

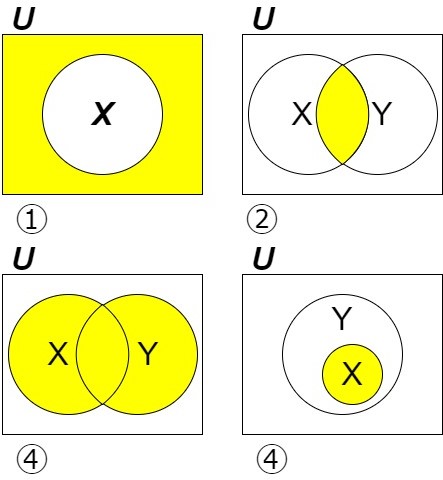
①$X$の補集合　②$X$と$Y$の共通部分　③　$X$と$Y$の和集合　$X$が$Y$の部分集合

（$U$は普遍集合です。）

この図示は直感的でですが、4個以上の集合では円が細長い棒状の奇妙な図形を書くことになり現実的ではありません。可視化していたことを、集合を定める述語をで認識することが重要です。

考察

それでは、定義した言葉を例を通して考えていきます。ただし、初等整数論での倍数の事実$$x \in \mathbb{Z}はnの倍数　\iff \exists k \in \mathbb{Z} (x=nk)$$を前提として用います。

まず、$n\mathbb{Z} \subset \mathbb{Z}$です。なので、1.から4.まですべて$\mathbb{Z}$の部分集合の中で考えていることになります。それぞれ、

1. 整数は偶数と奇数に分類できること
2. 述語の同値「$\exists k \in \mathbb{Z} (x=6k) \iff (\exists k \in \mathbb{Z} (x=2k) )\wedge (\exists l \in \mathbb{Z} (x=3l)))$」
3. 定義通り（特別な集合ではない）
4. 述語「$\exists k \in \mathbb{Z} (x=4k) \Rightarrow \exists l \in \mathbb{Z} (x=2l)$」

を利用しています。述語の真偽証明なので倍数の性質を用いて示してみてください。

和集合は、$2$と$3$の倍数すべての集合となっています。従って、他の集合と少し違うと感じると思います。この差は、数学の性質を崩すくせ者としてたびたび登場します。ただし、和集合と部分集合を組み合わせると、$$X \subset Y \Rightarrow X \cup Y =Y$$が成り立ちます。ベン図を考えれば当たり前ですが、これも述語を利用することで証明できます。

終わりに

今回は述語の言葉を使って集合の言葉を新しく定義できました。高校時代では、言語でいちいち説明していたことが、述語の記号だけで説明できることで労力を減らすことできます。証明では、すべて記号で書くことはできませんが、確認するときに「記述を減らせる」、「説明が必要なこと（述語）がわかる」というだけでも記述を知っておくことに意味があると思います。

次回は、小休憩として集合の元の一致を述語で説明できるようにします。

以上、ケンけんでした。