こんにちは!ケンけんです。前回は、命題の否定($not$)を記号化しました。
今回は、2つの命題を結ぶ「結合」と、複雑化する命題の真偽を確認する手段を取り扱います。
キーワード:「$P \Rightarrow Q$」(ならば)・真理値表
導入
二つの文章をつなぐ時、接続詞を学びました。そして、それは命題でも考えられるはずです。
- $a$が整数の時、「$a$は$6$の倍数である。だから$a$は$3$の倍数でもある。」
- とうもろこしはトウモロコシ属である。だからトウモロコシはイネ科である。
- 今年は、$111$人の入学者がいた。なので$100$人以上が入学してきた。
$6$の倍数を「$6$を約数に持つ数」とすると、$6$は$3$を約数に持つため$3$の倍数となります。
植物の科は属からわかるため、トウモロコシ属はイネ科だとわかります。
$100 \leqq 111$だから$111$人の入学者がいるとき、$100$人以上入学してきたことは明らかです。
この3つの文章は、正しいので真な命題です。
この命題は、「だから」の前を命題$P$、後ろを命題$Q$として、次の構図です。
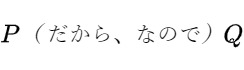
$P$から$Q$へ流れる文章なので、矢印「$\Rightarrow$」で「$P \Rightarrow Q$」と書いていきます。
次に、偽になる場合を考えましょう。
- $a$が整数の時、「$a$は$6$の倍数である。だから$a$は$5$の倍数でもある」
- アホウドリはアホウドリ科である。だからペンギン目である。
- 今年は、$111$人の入学者がいた。だから$44$名が男子、$67$名は女子だった。
$a=6$の時は$a$は$5$の倍数ではありません。アホウドリ科はミナヅキドリ目なので、ペンギン目ではありません。$45$名が男子、$66$名が女子の内訳もあり、入学者数だけでは内訳はわかりません。
これらの文章は例外があったり推論できず、「$P(だから、なので)Q$」で偽な命題です。
では、次の文章はどうでしょう。
明日西から陽が昇ったら、全財産を寄付します。
この文章は、「西から陽が昇る」ならば「全財産を寄付する」で「$P \Rightarrow Q$」の構造です。
先の例では「$P$が真の時の$Q$の真偽」が命題の真偽でした。
今の$P$側は偽だから、現状の「ならば」の使い方では判定不能です。
しかし、「$P \Rightarrow Q$」を使う上でルールを決めたいです。そこで次のように考えます。
この命題は、$$「西から陽が昇った」ときに「寄付しなかった」$$場合は嘘つきで偽です。今は前側が起こりえないので、$$「西から陽が昇った」ときに「寄付する」$$としか言っていないこの命題は嘘を言ったことにはなりません。
なぜなら、寄付する行為は「西から陽が昇った」場合だけであり「西から陽が昇らなかった」時のことは何も言っていないからです。二値論理から、偽ではない時は命題は真になります。
以上から「$P \Rightarrow Q$」は、
- $P$が真の時、「$Q$が真の時は命題は真」、「$Q$が偽の時は命題は偽」
- $P$が偽の時、命題は$Q$に関わらず真になる。
この議論は記号のルールを決めているだけで、実際は真な命題$P$の場合をを考えます。
定義
それでは、記号を定義しましょう。
$P$、$Q$;命題
$P \Rightarrow Q$($P \Leftarrow Q$);含意($implication$)
$$「P \Rightarrow Q」は「PならばQ」を表す命題$$
「$P \Leftarrow Q$」の時は「$Q$ならば$P$」を表す命題になる。
否定($\neg$)と同様に、「$P \Rightarrow Q$」も$P$と$Q$の真偽から決まる新しい命題です。
この表現は「必要条件と十分条件」で高校で苦しめられた人が多いでしょう。
命題「$p \Rightarrow q$」が成り立つとき、
$$pはqであるための十分条件である$$
$$qはpであるための必要条件である$$
という。
東京書籍 NEW ACTION LEGEND 思考と戦略 数学Ⅰ+A p84
私は、「今$Q$の性質が必要だ。(必要条件)それを真にするためには条件$P$が成り立てば十分だ。(十分条件)」として覚えていました。
数学の定理は$P$が真の時に使うものであり、構造を理解すればこの二つの条件も理解できます。例えば次の例があります。
$a \neq 0$ 無限等比級数$S=\sum ar^n$
$|r|< 1 \Rightarrow S=\frac{a}{1-r}$
$|r| \geq 1 \Rightarrow 「Sは発散」 $
この例に、例2-3で議論した前側が偽の場合の扱いが隠れています。
$|r|< 1$の時に下の条件は使いません。
なぜなら、前提条件が偽で性質は意味がなく、持ち出す必要がないからです。
逆に、$|r| \geq 1$の時は、下側の命題を使うでしょう。
2つの条件を「$P \Rightarrow Q$」とみると、$P$が真の時はどちらも真の命題です。$P$が偽の時、は常に真で役に立たないので議論には使わず気にしません。例2-3の議論が面倒と思ったでしょうが、実は定理や性質を使うときに自然とあの議論をしていたのです。
また、必要な性質は$Q$(必要条件)の$S$が収束するかどうかで、そのために成り立てば十分な条件である$r$の性質が$P$(十分条件)となっています。ここから、必要条件と十分条件の関係が見えます。
真偽の確認手段
ここまで、命題の否定と含意を定義しましたが、真偽が複雑になり始めています。また個別の命題をいちいち調べる手間があります。
そこで、命題の内容を無視して真偽だけを取り出します。そして、真偽だけで表を作ると全体を眺めやすくなるでしょう。
$P$は命題変数($proposition \ variable$) $\overset{def}{\iff}Pは命題$
真理値($truth \ value$);命題変数の真偽で決まる文字
- 命題変数「$P$」が真の時、真理値は$T$である。
- 命題変数「$P$」が偽の時、真理値は$F$である。
真理値表;命題変数の真理値を記述した表
命題変数で考えると以下のように真理値表が作れます。
| $P$ | $Q$ | $\neg P$ | $\neg Q$ | $\neg (\neg P)$ | $ P \Rightarrow Q$ | $ \neg (P \Rightarrow Q)$ | $ \neg P \Rightarrow Q$ | $ P \Rightarrow \neg Q$ | $ \neg P \Rightarrow \neg Q$ |
| $$T$$ | $$T$$ | $$F$$ | $$F$$ | $$T$$ | $$T$$ | $$F$$ | $$T$$ | $$F$$ | $$T$$ |
| $$T$$ | $$F$$ | $$F$$ | $$T$$ | $$T$$ | $$F$$ | $$T$$ | $$T$$ | $$T$$ | $$T$$ |
| $$F$$ | $$T$$ | $$T$$ | $$F$$ | $$F$$ | $$T$$ | $$F$$ | $$T$$ | $$T$$ | $$F$$ |
| $$F$$ | $$F$$ | $$T$$ | $$T$$ | $$F$$ | $$T$$ | $$F$$ | $$F$$ | $$T$$ | $$T$$ |
どんな$P$と$Q$でも、この表の$T$と$F$は変わらないので一般の性質が記述できるわけです。この表は大きいですが、必要な部分だけ書くと見やすくなります。
これを書かずに真偽判定ができるなら、論理関係はかなり慣れてきていると言えます。
おわりに
筆者は大学1年次に集合論のゼミに参加したのですが、「$\Rightarrow$」の前側が偽の時の解釈は最も苦労した部分です。今回の説明も何度も書き直しています。読んでくださった方は、自分が納得できる例を考えてみてください。高校数学の話を少し挙げましたが、もう一度数学Ⅰの教科書を眺めてみるのも効果的です。また、記事の真理値表は、一部なので上の表以外の組み合わせも実際に手で書いてみてください。
次回は、命題の結合2つ目、論理の足し算・掛け算?を取り扱います。
以上、ケンけんでした。
参考文献
・東京書籍 NEW ACTION LEGEND 思考と戦略 数学Ⅰ+A

