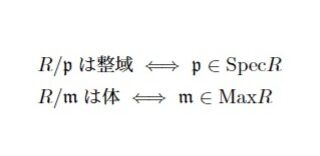 代数基礎
代数基礎 BR1-10:乗法が不完全だから起こること 零因子・整域・体
零因子・整域・体 環の乗法はイデアルを部分加群と見た時の作用と同じである.ここから,作用と同様に零因子を定義できる.環の場合は同じ集合同士の演算のため,環本体により強い制約を付けることができる.今回は,加群の概念から拡張する形で環の零因子を定義し特別な環である整域と体の議論をいくつか挙げる.
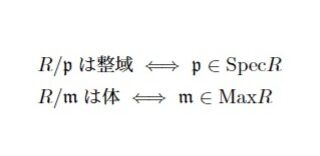 代数基礎
代数基礎  位相構造
位相構造  加群基礎
加群基礎 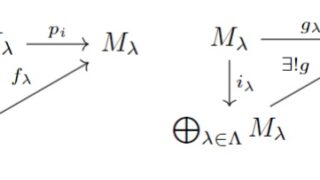 加群基礎
加群基礎 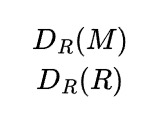 加群基礎
加群基礎 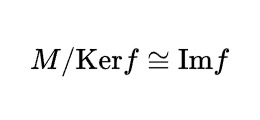 加群基礎
加群基礎  加群基礎
加群基礎 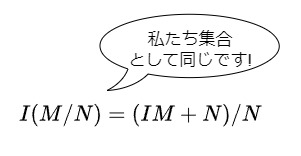 加群基礎
加群基礎 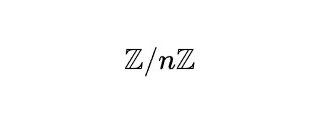 代数基礎
代数基礎 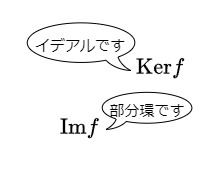 代数基礎
代数基礎