 学習帳
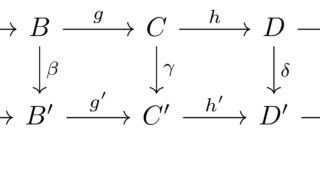
学習帳 MOD-L-6:蛇じゃない方の強い道具 Five Lemma
Five Lemma 完全列の主張ではFive LemmaとSnake Lemmaの2つがあり前者を利用しtorsion-freeとdivisibleの完全列の情報保存について示そうと思った。しかし、前回の一方向しか示せない。試行錯誤した結果、反例を見つけた。記事後半では、うまくいかない理由を証明の観点から考察する。
 学習帳
学習帳  学習帳
学習帳  位相構造
位相構造 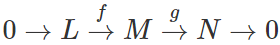 学習帳
学習帳  素朴集合論(NST)
素朴集合論(NST) 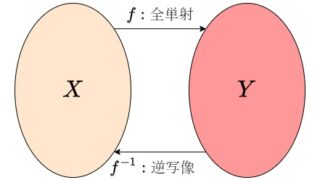 素朴集合論(NST)
素朴集合論(NST) 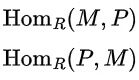 学習帳
学習帳  学習帳
学習帳