 加群基礎
加群基礎 MOD1-5:加群の生成と有限生成性 生成された部分加群
生成された部分加群 イデアルと同様に、特定の部分集合を含む最小の加群として生成された部分加群が定義される。こちらも有限生成を考えることができるがその側面はイデアルの場合と異なるものがある。今回は、生成された部分加群を定義するとともに線形代数における基底と環上の加群での生成系について考える。
 加群基礎
加群基礎  加群基礎
加群基礎  代数基礎
代数基礎  代数基礎
代数基礎 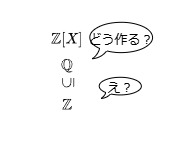 代数基礎
代数基礎 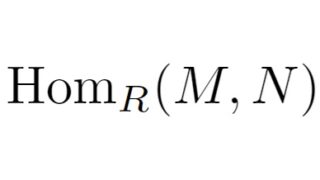 加群基礎
加群基礎 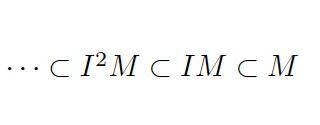 加群基礎
加群基礎 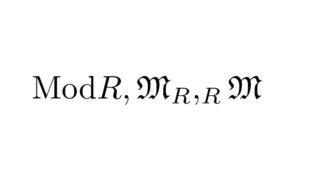 加群基礎
加群基礎  学習帳
学習帳  可換環論
可換環論